
SAT Math formulas - Tổng hợp các công thức thường gặp trong SAT Math
Người học đang chuẩn bị cho kỳ thi SAT chắc hẳn cảm thấy đôi chút áp lực khi đối mặt với phần thi Toán. Đây là phần khiến nhiều thí sinh phải băn khoăn nhất, bởi nó yêu cầu thí sinh phải trong trạng thái sẵn sàng giải nhiều dạng bài tập khác nhau trong một khoảng thời gian nhất định. Tuy nhiên, với sự chuẩn bị kỹ lưỡng và việc nắm vững các công thức cơ bản, thí sinh có thể dễ dàng vượt qua phần thi này với điểm số cao.
Trong bài viết dưới đây, ZIM sẽ hướng dẫn qua 30 công thức thường gặp của SAT Math trong cả phần đại số và hình học, cùng với giải thích ngắn cho mỗi khái niệm.
Key takeaways
Các công thức phần Đại số trong SAT Math:
Căn bản về Đại số:
Ước số; Bội số
Đo độ dài của một đoạn thẳng trên mặt phẳng toạ độ
Phương trình tuyến tính
Nhân hai đa thức
Hằng đẳng thức đáng nhớ
Giá trị tuyệt đối
Hệ phương trình bậc nhất 2 ẩn
Phương trình bậc hai
Xác suất thống kê:
Trung bình cộng
Tốc độ trung bình
Xác suất
Phần trăm
Lãi suất đơn
Lãi suất kép
Các công thức phần Hình học trong SAT Math:
Chu vi và diện tích hình tròn; Độ dài cung tròn; Diện tích của một phần hình cung
Diện tích hình chữ nhật
Diện tích hình tam giác
Định lý Pythagoras (Py-ta-go)
Tam giác vuông đặc biệt
Thể tích của hình hộp chữ nhật
Thể tích của hình trụ
Thể tích của hình cầu
Thể tích của hình nón
Thể tích của hình chóp
Các công thức phần Lượng giác trong SAT Math:
Lượng giác trong tam giác vuông
Công thức lượng giác
SAT Math formulas phần Đại số
Căn bản về đại số (Heart of Algebra)
Ước số (Factors)
Các ước số của một số chia hết cho số đó mà không bị dư.
Ví dụ: Ước số của 57 là 1, 3, 19, và 57.
Bội số (Multiples)
Các bội số của một số chia hết cho số đó mà không bị dư phần.
Ví dụ: Bội số của 57 là 57, 114, 171, 228, 285,…
Đo độ dài của một đoạn thẳng trên mặt phẳng toạ độ (Distance Formula)
Đây là công thức dựa trên định lý Pytago, người học có thể xem đoạn thẳng cho trước như là cạnh huyền của tam giác vuông.
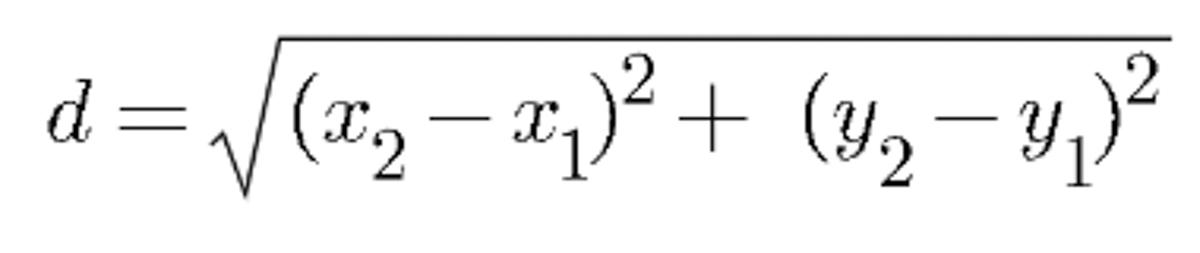
Trong đó:
d: độ dài của một đoạn thẳng
x1, y1: tọa độ điểm đầu tiên của đoạn thẳng
x2, y2: tọa độ điểm thứ hai của đoạn thẳng.
Phương trình tuyến tính (Linear Equation)
y = m x + b
Trong đó:
m: độ dốc của đường thẳng. Giá trị dương của m cho thấy đường thẳng nghiêng lên bên phải, trong khi giá trị âm của m cho thấy đường thẳng nghiêng xuống bên phải.
x là giao điểm của y.
b: hằng số (hay hệ số bậc 0).
Ví dụ phương trình y = 2x - 6 thì có m = 2 và giao điểm trục tung là (0,-6).
Nhân hai đa thức
Người học nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia sau đó cộng các tích lại với nhau.
Hằng đẳng thức đáng nhớ

Giá trị tuyệt đối (Absolute Values)

Trong đó:
x là số nguyên vì giá trị tuyệt đối của một số luôn là số dương.
Ví dụ:
|3| = 3
|-3| = 3
Hệ phương trình bậc nhất 2 ẩn (Systems of equations 2 variables)

Trong đó:
a, a’, b, b’: các số thực cho trước khác 0
x,y: ẩn số.
Nếu a’, b’, c’ = 0 thì đưa về các trường hợp đặc biệt.
Nếu a’, b’, c’ khác 0 thì:
Hệ phương trình có nghiệm khi:

Hệ phương trình vô nghiệm khi:

Hệ phương trình vô số nghiệm khi:

Phương trình bậc hai (Quadratic equation)
Nếu

nhưng a khác 0
thì ⇒

Trong đó:
Nếu biệt thức đen-ta là dương thì có 2 nghiệm
Nếu biệt thức đen-ta = 0 thì có 1 nghiệm
Nếu biệt thức đen-ta là âm thì có không có nghiệm.
Xác suất thống kê (Problem Solving and Data Analysis)
Trung bình cộng (Arithmetic mean)

Trong đó:
a: số trung bình cộng
a1, a2, a3,.. an: tổng của số hạng
N: số của số hạng.
* Lưu ý: Cần cẩn thận phân biệt giữa mean (trung bình thực tế) và median (trung vị).
Trung vị là số nằm giữa trong một tập dữ liệu có dãy số được sắp xếp theo giá trị từ thấp nhất đến cao nhất, hoặc ngược lại. Trung vị có thể được sử dụng để xác định giá trị trung bình gần đúng hoặc giá trị trung bình.
Ví dụ: Trong tập dữ liệu 3, 1, 4, 2, 5, các số được sắp xếp từ nhỏ đến lớn là 1, 2, 3, 4, 5. Trong trường hợp này, trung vị là 3 vì nó ở giữa.
Trong tập dữ liệu: 3, 1, 4, 2, 5, 6, các số được sắp xếp là 1, 2, 3, 4, 5, 6. Vì có hai giá trị ở giữa (3 và 4), trung vị là (3 + 4) / 2 = 3.5.
Tốc độ trung bình (Average speed)

Xác suất (Probability)
Xác suất đại diện cho tỉ lệ một việc có thể xảy ra.
* Lưu ý: Xác suất = 1 đảm bảo việc đó sẽ xả ra. Xác suất = 0 xác định việc đó sẽ không diễn ra.
Phần trăm (Percentages)
Tìm x phần trăm của một số n đã cho.

Ví dụ: Tìm 20% của số 80.
→ A = (20/100) * 80 = 16.
Tìm phần trăm mà số n đó trong số m khác.

Ví dụ: Tìm phần trăm mà 15 chiếm trong số 60.
→ A = (15/60) * 100 = 25%.
Tìm số mà nó chiếm x phần trăm trong tổng.
Ví dụ: Tìm số mà 40% chiếm trong tổng là 120.
→ A = (40/100) * 120 = 48.
Lãi suất đơn (Simple Interest)
Dù dạng bài này ít xuất hiện hơn dạng Lãi suất kép nhưng chúng vẫn có thể xuất hiện. Vì vậy, người học vẫn nên nắm chắc công thức cơ bản này.
A = P . r . t
Trong đó:
A: số tiền cuối cùng
P: số vốn ban đầu
r: tỷ lệ lãi suất
t: thời gian, thường tính bằng năm.
Lãi suất kép (Compound Interest)

Trong đó:
A: số tiền cuối cùng
P: số vốn ban đầu
r: tỷ lệ lãi suất
t: thời gian, thường tính bằng năm
n: số lần lãi suất được tích lũy trong t thời gian.
Ví dụ, nếu lãi suất được tích lũy theo từng quý trong vòng một năm, thì n sẽ là 4.
Tham khảo thêm: Những điều cần biết về Math Test SAT và các thuật ngữ Toán Đại Số.
SAT Math formulas phần Hình học
Hình tròn

Chu vi của một vòng tròn (Circumference of a Circle)

Trong đó:
C: chu vi của một vòng tròn
π: số pi, thí sinh có thể sử dụng giá trị gần đúng là 3.14 hoặc 3.14159
r: bán kính của hình tròn (đoạn thẳng từ trung tâm của hình tròn đến lề của hình).
Diện tích hình tròn (Area of a Circle)

A: diện tích hình tròn.
Độ dài cung tròn (Length of an arc)

Trong đó:
l: độ dài cung tròn
π: số pi
r: bán kính đường tròn
n: số đo góc của cung.
Diện tích của một phần hình cung (Area of an arc sector)

* Lưu ý: Một vòng tròn có số đo là 360 độ.
Diện tích hình chữ nhật (Area of a Rectangle)

Trong đó:
A: diện tích hình chữ nhật
l: chiều dài hình chữ nhật.
w: chiều rộng hình chữ nhật.
Diện tích hình tam giác (Area of a Triangle)

Trong đó:
A: diện tích hình tam giác
b: chiều dài cạnh đáy tam giác
h: chiều cao tam giác.
Định lý Pythagoras (Py-ta-go) (The Pythagorean Theorem)

Trong tam giác vuông,
a,b: hai cạnh nhỏ
c: cạnh lớn nhất
Tam giác vuông đặc biệt
Tính chất của tam giác vuông 30, 60, 90 độ (30, 60, 90 Degree Triangle):

30, 60, 90 độ mô tả các độ đo của ba góc tam giác.
Chiều dài của các cạnh được xác định bằng công thức: x, x√3, 2x.
Cạnh đối diện với góc 30 độ là cạnh nhỏ nhất, với độ đo là x.
Cạnh đối diện với góc 60 độ là cạnh trung bình, với độ đo là x√3.
Cạnh đối diện với góc 90 độ là đường chéo (cạnh dài nhất), với độ đo là 2x.
Ví dụ: Một tam giác vuông 30, 60, 90 độ có chiều dài các cạnh là 7, 7√3, và 14.
Tính chất của tam giác vuông cân (Isosceles Triangle):

Một tam giác vuông cân luôn có một góc 90 độ và hai góc 45 độ.
Một tam giác vuông cân có hai cạnh gần góc vuông có độ dài bằng nhau.
Chiều dài của các cạnh được xác định bằng công thức: x, x, và x√2.
Ví dụ: Một tam giác vuông cân có chiều dài cạnh là 10, 10 và 10√2.
Thể tích của hình hộp chữ nhật (Volume of a Rectangular Solid)

Trong đó:
V: thể tích hình hộp chữ nhật
l: chiều dài của một trong các cạnh
w: chiều rộng của một trong các cạnh
h: chiều cao của hình hộp.
Thể tích của hình trụ (Volume of a Cylinder)

Trong đó:
V: thể tích hình trụ
π: số pi
r: bán kính của bề mặt tròn hình trụ.
h: chiều cao hình trụ.
Thể tích của hình cầu (Volume of a Sphere)

Trong đó:
V: thể tích hình cầu
π: số pi
r: bán kính hình cầu.
Thể tích của hình nón (Volume of a Cone)

Trong đó:
V: thể tích hình nón
π: số pi
r: bán kính bề mặt tròn của hình nón
h: chiều cao phần nhọn của hình nón (đo từ trung tâm của phần tròn của hình nón).
Thể tích của hình chóp (Volume of a Pyramid)

Trong đó:
V: thể tích hình chóp
l: chiều dài của đáy
w: chiều rộng của đáy
h: chiều cao hình chóp (đo từ trung tâm của phần hình chữ nhật của hình chóp).
* Lưu ý:
Đơn vị radian trong một vòng tròn là 2π → Nếu người học muốn đổi độ sang radian thì cần lấy π/180
Tổng ba góc của một tam giác luôn bằng 180 độ → Tam giác đều có ba cạnh bằng nhau, và cả ba góc bằng 60 độ.
 Nguồn: SAT Study Guide - College Board
Nguồn: SAT Study Guide - College Board
SAT Math formulas phần Lượng giác
Lượng giác trong tam giác vuông (Right Triangle Trigonometry)
Trong tam giác vuông có chứa góc A, các cạnh được đặt tên như sau:
Cạnh huyền là cạnh đối diện với góc vuông, là cạnh dài nhất của tam giác vuông.
Cạnh đối là cạnh đối diện với góc A.
Cạnh kề là cạnh nối giữa góc A và góc vuông.
Sin = cạnh đối chia cạnh huyền
Cos = cạnh kề chia cạnh huyền
Tan = cạnh đối chia cạnh kề
Cotan = cạnh kề chia cạnh đối
Công thức lượng giác (Trigonometric Identities)
Sau đây là một số công thức lượng giác cơ bản người học nên nhớ:

Tổng kết
Chinh phục phần Toán trong kỳ thi SAT có thể là một nhiệm vụ đầy thách thức, nhưng với 30 SAT Math formulas - 30 công thức đại số và hình học cơ bản này trong tay, người học đã chuẩn bị tốt bước đầu tiên cho sự thành công. Hãy nhớ rằng việc luyện tập thường xuyên với các công thức trên là nền tảng quan trọng để hoàn thành bài thi thật tốt.
Người đọc tham khảo thêm:
Phương pháp giải các dạng bài trong SAT Math (P1)
Phương pháp giải các dạng bài trong SAT Math (P2)
Phương pháp giải các dạng bài trong SAT Math (P3)
Học sinh được hỗ trợ giải đáp thắc mắc, chữa bài tập trên diễn đàn ZIM Helper bởi các Giảng viên chuyên môn đang giảng dạy tại ZIM.
Link nội dung: https://tulieutieuhoc.edu.vn/toan-sat-a72547.html